SQL勉強メモ

SQL関連で勉強したことのまとめ記事。
長くなってきたのでリンク集として使っていきたい。

SQL実行順序

FROM
JOIN
WHERE
GROUP BY
SUM, MAXなど
HAVING
SELET,DISTINCT
ORDER BY
LIMIT

ちなみにサブクエリは内側から最初に実行される。

小技集

select 1

select 1 from table～という謎のSQLに出会った。

exists文で使われるものらしい。

存在するかどうかだけがわかればよくて、データは要らないよって時に使う。

ただ、select 1 より select * のほうが早いらしい↓
COUNT(*)とCOUNT(1)の処理速度検証結果

もっと言うとexistsよりjoinのほうが早いらしい↓
EXISTSとSQLの高速化について - 猫好きモバイルアプリケーション開発者記録

-- A.name = B.nameである行だけ抽出
select * from Atable AS A
where
exists(
    select 1 from Btable AS B
    where
    A.name = B.name
    )

-- -- A.name = B.nameではない行だけ抽出
select * from Atable AS A
where
not exists(
    select 1 from Btable AS B
    where
    A.name = B.name
    )

where 1 = 1

where はtrueかfalseかで判定している。

1 = 1なら常にtrue。

使い所はwhere句かand句かの分岐の時。

よく複数単語検索なんかで使う。

検索条件が増える度にAND句で追加したいんだけど、最初はWHERE句じゃないといけないのでめんどくさい。

そこで WHERE句を1＝1にして、AND句の追加だけで良いようにする。

select * from
where 1= 1
and~ // ここに追加していく

・参考サイト
「WHERE 1=1」は条件付きSQL文が書きやすくなる魔法の言葉 | キノコログ

OFFSET FETCH

MySQLのLMIT OFFSETと同じで取得する行数を指定できる。

OFFSETでスキップする行数を指定。
FETCH NEXT ○ ROWS ONLYで何行取得するかを指定。

select user_id, name from account_table
order by user_id
OFFSET 10 ROWS
FETCH NEXT 5 ROWS ONLY;

11行～15行を取得。

・参考

sql-oracle.com

count(*)over()

window関数。

ページングの時にとても便利！

selectで総レコード数を取得しつつ、1ページ分のselect結果も欲しいときに使える。

secect count(*)over() , account_name
from account
limit 0 rows
fetch 100 rows

・参考記事

resanaplaza.com

テーブルデータ増殖技(Insert Select)

増殖テーブル

・SQL
id = A　を　id = B　にしてそれ以外の列はそのままで増殖する。

insert into increse
select 
name,
'B'
from increse
where
id = 'A'

増殖後

イメージとしては下記SQLを実行している感じ。
INSERT INTO table (name, id) VALUES (SELECT文)

insert into increse
(name, id)
values
(select name, 'C' AS 'id' from increse
where 
id = 'B')

GROUP BY句にないカラムも表示させたい

Group By句にないカラムを表示させたい - okinawa

テーブル同士の比較

【SQL】テーブル同士の比較 - okinawa

基礎知識

GROUP BYってなんなの？

部分集合に切り分ける。
GROUP BYってなんなの？ - okinawa

NULLとの四則演算は必ずNULLになる

1 + NULL = NULL
5 * NULL = NULL

集合指向言語と手続き型言語の違い

集合指向言語：まとめて処理
手続き型言語：１件ずつ処理
集合指向言語と手続き型言語の違い - okinawa

HAVING句を理解すると集合志向が理解できるらしい

HAVING句をマスターすると集合志向が理解できるらしい - okinawa

３値論理

普通は TRUE/FALSEの２つ
SQLは TRUE / FALSE / UNKNOWN の３つ
真理値の優先順位は下記↓

• AND：FALSE > UNKNOWN > TRUE
• OR： TRUE > UNKNOWN > FALSE

【SQL】３値論理とは - okinawa

バッファプールとログバッファ

• バッファプール：ストレージ（HDD)にあるRDBのデータの一部を保持している。
• ログバッファ：更新処理のときに更新情報をログバッファ上にためて、コミット時にまとめて行うための領域。

バッファプールとログバッファ - okinawa

豆知識

COUNT(＊)とCOUNT(列名)の違い

• COUNT(＊)：NULLも含む全行カウント
• COUNT(列名)：NULLではない行数カウント

ちなみにAVG()はNULLの行はカウントしないで計算する。

相関名（AS～）の有効範囲

（）内の名前は（）の内側のみで使用可能。
外側では使用不可。

これは実行順序の問題。
サブクエリは内側から実行される。
実行された後は実行結果しか残らないので名前はもう残っていない。。。
なんかかっこいい。

ほかにもSELECT句でつけたAS名がWHERE句で使えないのもSELECT句の方が実行順序が後だから。

UNIONの使い所

異なるテーブルをまとめて集計したいとき。
UNIONの使い所 - okinawa

CASE式のELSE句は必ず書くべし！

ELSEは省略するとNULLが入ってしまうので。
SQL CASE式について - okinawa

サブクエリの実行順序と相関サブクエリ

サブクエリは内側から実行される。
SQL サブクエリについてのメモ - okinawa

特性関数とは

ある値が集合に含まれるか調べる関数。
集合に対する条件判定や集計に便利な関数です。
【SQL】特性関数とは - okinawa

SQLチューニング

実行計画の見方。

• MySQLはSQL文の頭に　explain　を付けるだけ。
• SQLServerはSQL文の頭に　SET STATISTICS PROFILE ON　を付ける。

GUIで見る方法もある↓

実際の実行プランの表示 - SQL Server | Microsoft Learn

チューニングについては過去記事も参照↓

GMOのDBチューニング課題やってみた - okinawa

インデックスって何なの？

DB勉強メモ - okinawa

SQLチューニング方法一覧

SQLチューニングの一覧 - okinawa

統計情報とは

実行計画を練るためのネタ元

統計情報とは - okinawa

テーブル結合関連

inner join と outer joinの違いはベン図で表すとわかりやすい

ベン図

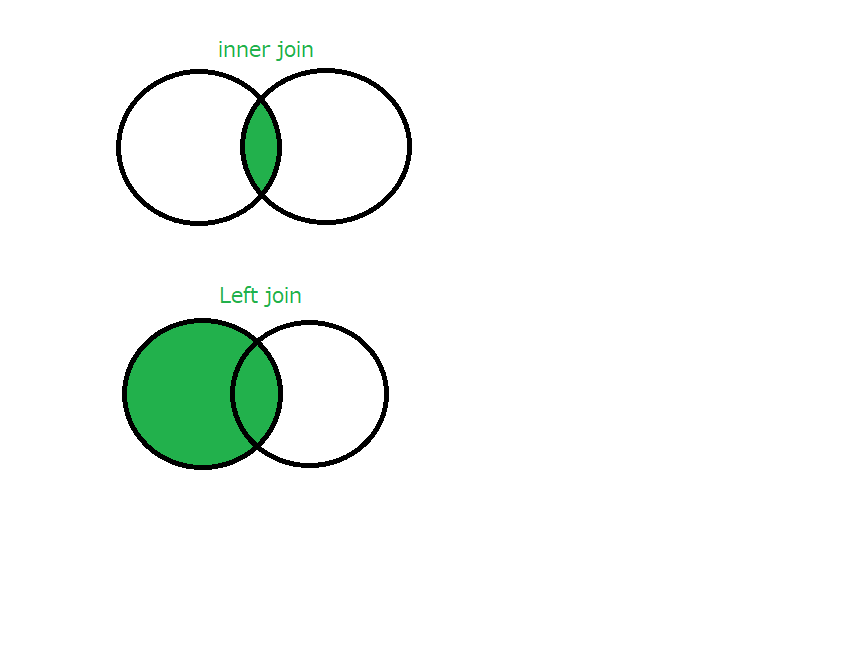
・参考記事
SQL Joinサンプル集 Joinで遅いSQLの原因を調べる方法 | ポテパンスタイル

Isn't SQL A left join B, just A? - Stack Overflow

on句が一部合致するとどうなるの？

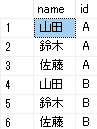
下記の2テーブルをleft outer joinで実験。

Shohinテーブル

Zaikoテーブル

select * from Shohin
left outer join Zaiko
on Zaiko.name = Shohin.shohin_mei
and Zaiko.category = Shohin.shohin_bunrui;

・結果

on句が全部合致した行だけ値が入って結合されている。1行目と3行目。

on句が一部合致した行は全部nullで結合されている。4行目。

すべて合致した行のみ結合され、それ以外はNULLで出力されるということ。

結果

on句をwhere句っぽく使うときの注意点

・torihikijiyuテーブル

取引事由テーブル

・haishi_kouzaテーブル

廃止口座テーブル

・SQL文(right outer join)

select * from haishi_kouza
right outer join
torihikijiyu as tor
on
tor.torihikijiyumei = '契約' --where句っぽいところ

結合後2

上記のように取引事由が「契約」以外の行も出力されてしまう。
right joinの場合は右側のテーブルは結合条件に合致しなくても全て出力される。
そのためtorihikijiyuテーブルの行はすべて出力。

この場合は、leftかinner joinにすれば取引事由が「契約」の行のみ出力される。

あれ？どゆこと？ where句と同じことになると思ってたけどそうじゃないようで。
どうやらouter側のテーブルは全部返ってくる。
でも inner joinの時はwhere句みたいな動きをしている。（SQL1） ま、where句みたいに使いたいならwhere句を使いましょう。
→where句よりjoin句で絞り込んだほうが処理が早いらしい。

・SQL文1(left join)

select * from haishi_kouza
left join
torihikijiyu as tor
on
tor.torihikijiyumei = '契約'

結合後

結果は廃止口座テーブルの全ての行に取引事由テーブルの「契約」の行だけが結合される。

ここのまとめ

結合の向きに注意する。

・tableA left join tableB
tableB.columnB = '契約' にすると「契約」の行のみ結合して出力。

・tableA right join tableB
tableB.columnB = '契約' にすると「契約」以外の行も全て出力されてしまう。

テーブル結合ってなんなの？（重要）

無条件テーブル結合をやってみたらわかりやすかった。

・torihikijiyuテーブル

取引事由テーブル

・haishi_kouzaテーブル

廃止口座テーブル

・SQL（無条件結合）

select * from haishi_kouza
inner join
torihikijiyu as tor
on
1 = 1

・結果

結合後

テーブル結合ってのは
列は、tableA + tableB
行は、tableA × tableB
になるんだなあ。

外部結合ミスの見つけ方

外部結合が上手くいってなくて不要な行が出力されたり、nulで出力されて困った時に。

• nullではないはずのカラムがnullだったら外部結合ミスを怪しもう。ON句の結合ができない行はnullを含んで出力される。
• 妙なところにMAXやMINが使われていたら外部結合ミスを取り繕っている可能性あり

テーブル結合で行を増殖させないポイント

ON句の条件を

• 1対1で結合
• 1対多で結合

【SQL】テーブル結合で行を増殖させないポイント - okinawa

集合演算をテーブル結合でやってみる

SQLの集合演算をテーブル結合でやってみる

テーブル結合ハマったこと

テーブル結合でハマったこと - okinawa

SQLを読むときのポイント

• 最初にSELECT行を見て何を取得するか把握する
• 最初のFrom句のテーブルがメインテーブル
• group byやsumなどの集約関数を見ると何を集計したいのかわかる
• ネストの深いところから見ていくと割とわかりやすい

SQLテストサイト

ブラウザでSQLを実行できる便利サイト↓
sqlfiddle.com

その他

DISTINCTとNOT EXISTSでハマった話

NOT EXISTSとDISTINCTでハマった話 - okinawa

座標圧縮

座標圧縮とは

値が何番目に小さいかをナンバリングする。

例えば、下記のX座標が何番目に小さいかを知りたい時に使う。
元の並び順を維持したままいける。

X = [8, 50, 33, 33, 33, 12, 1, 777]#1 4 3 3 3 2 0 5

ソースコード

重複を集合で除去　➯　連想配列に{key=圧縮前, value=圧縮後}を格納　➯　圧縮前配列をkeyにして、圧縮後連想配列を参照

#X座標の配列
X = [8, 50, 33, 33, 33, 12, 1, 777]

# 重複除去＆ソート
B = sorted(set(X)) # [1, 8, 12, 33, 50, 777]

# 昇順で何番目かを連想配列のvalueに記録。key:圧縮前の座標 value:圧縮後の座標（何番目）
ranking = { before: i for i, before in enumerate(B) }
# {1: 0, 8: 1, 12: 2, 33: 3, 50: 4, 777: 5}

# 元の順番を維持したまま、座標圧縮
for Xi in X:
    print(ranking[Xi], end=" ") #1 4 3 3 3 2 0 5

例題

正に座標を圧縮する問題。

atcoder.jp

参考サイト

qiita.com

動的計画法

まだ、初歩的な部分に触れただけなので追記したい。

動的計画法とは

動的計画法（どうてきけいかくほう、英: Dynamic Programming, DP）は、計算機科学の分野において、アルゴリズムの分類の1つである。対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法を総称してこう呼ぶ。

細かくアルゴリズムが定義されているわけではなく、下記2条件を満たすアルゴリズムの総称である。

1、帰納的な関係の利用：より小さな問題例の解や計算結果を帰納的な関係を利用してより大きな問題例を解くのに使用する。
2、計算結果の記録：小さな問題例、計算結果から記録し、同じ計算を何度も行うことを避ける。帰納的な関係での参照を効率よく行うために、計算結果は整数、文字やその組みなどを見出しにして管理される。

動的計画法 - Wikipedia

自分の理解

現在地に至るまでの１個手前の選択肢を全部考える。

再帰関数と考え方が似ている気がする。

実際、フィボナッチ数列を動的計画法で作れるようです。

Fib=[0]*10
Fib[1]=1

for i in range(2,10):
    Fib[i] = Fib[i-1] + Fib[i-2]

print(*Fib) # 0 1 1 2 3 5 8 13 21 34

例題

初めて触れた動的計画法で解く問題。
わかりやすいコードで解ける、教育的で良い問題だと思った。
atcoder.jp

例題の解答コード

n,k=map(int,input().split())
a=list(map(int,input().split()))
b=list(map(int,input().split()))

dp=[[False]*n for _ in range(2)]

dp[0][0]=True
dp[1][0]=True

for i in range(1,n):
    #a[i-1]がTrueなら、a[i]へいけるか、b[i]へ行けるかを考える
    if dp[0][i-1]:
        #a[i-1]からa[i]へいけるか？
        if abs(a[i-1] - a[i]) <= k:
            dp[0][i] = True
        #a[i-1]からb[i]へいけるか？
        if abs(a[i-1] - b[i]) <= k:
            dp[1][i] = True

    #b[i-1]がTrueなら、a[i]へいけるか、b[i]へ行けるかを考える
    if dp[1][i-1]:
        #b[i-1]からa[i]へいけるか？
        if abs(b[i-1] - a[i]) <= k:
            dp[0][i] = True
        #b[i-1]からb[i]へいけるか？
        if abs(b[i-1] - b[i]) <= k:
            dp[1][i] = True



if dp[0][n-1] or dp[1][n-1]:
    print("Yes")
else:
    print("No")

参考サイト

動的計画法ってなに？ (導入) | アルゴ式

【ゆっくり解説】DP(動的計画法)解説 EDPC D 【競技プログラミング】 - YouTube

ABC245 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder - Qiita

【Python】cmp_to_keyでソートの実装

cmp_to_keyの実装

比較対象の2つの値を引数として、第一引数が第二引数よりも小さければ負の値、大きければ正の値、等しければ0を返すように実装します。

from functools import cmp_to_key

def compare(arg1, arg2):
    #数値を昇順ソート
    if arg1 == arg2: return 0
    if arg1 < arg2: return -1
    if arg1 > arg2: return 1

ls=[3,0,2,1]
ls = sorted(ls, key=cmp_to_key(compare))
print(ls)

例題

atcoder.jp

参考サイト

functools — Higher-order functions and operations on callable objects — Python 3.11.4 documentation

Python 3のsorted関数と比較関数 - Qiita

Pythonのデータソートについて検証してみた | DevelopersIO

幅優先探索＆最短経路復元＆距離計測

幅優先探索（BFS）とは

幅優先探索とは、グラフや木構造を探索するためのアルゴリズムの一つで、探索を開始する頂点から近い順に探索する方式。　

幅優先探索（BFS / 横型探索）とは - 意味をわかりやすく - IT用語辞典 e-Words

使い所

最短経路問題

ソースコード

経路復元と距離計測もあり。

・経路復元は何をしているのか？
配列を辿っていっている。

例：配列A　A[現在地] = 次の目的地

1. A[5] = 3：現在地＝5。次の目的地３なので、A[3]に移動
2. A[3] = 1：現在地＝3。次の目的地1なので、A[1]に移動
3. A[1] = 0：現在地＝1。次の目的地0なので、A[0]に移動
4. A[0]：0に到着

from collections import deque

n = int(input())
g=[[] for _ in range(n)]
Q=deque()
seen=[False]*n #探索済チェック用
dist=[0]*n #距離計測用
previous =[0]*n #探索経路用

#入力の受け取り
for i in range(n-1):
    u,v=map(int,input().split())
    u=u-1
    v=v-1
    g[u].append(v)
    g[v].append(u)

Q.append(0)#始点をキューに追加
previous[0] = -2 #始点には-2
while(len(Q)) > 0:
    vertex = Q.popleft() #先入れ先出し
    #vertex = Q.pop #後入れ先出し
    seen[vertex] = True

    for next in g[vertex]:
        if seen[next]: continue #探索済みはスルー
            
        dist[next] = dist[vertex] + 1 #距離を格納

        #探索経路を1つ前の頂点を追加
        previous[next] = vertex

        Q.append(next)#キューに次を追加

ans = []
now = 5 #頂点5から始点までの最短経路復元
ans.append(now - 1)
while previous[now] != -2:
    now = previous[now]
    ans.append(now + 1)

# 最短経路を出力
print(*ans[::-1])

参考サイト

kunassy.com

例題

C - Simple path

D - .. (Double Dots)

bit全探索【Java,Python】

理解するのに苦労したので、忘れないようにメモ。

使い所

選択する or 選択しないの2択を組み合わせ全探索するとき。

参考サイト

qiita.com

algo-method.com

Java

「1 << N」 は２のN乗。

「S & (1 << i))」は整数Sを2進数とみなして、下からi桁目が1か判定。

簡単に言うと、８通り全探索したいなら、0～8を順番に2進数に変換して、１になったとこだけ選択する。

import java.io.IOException;
import java.util.Scanner;

//Q2. 部分和問題　https://algo-method.com/tasks/1083
public class BitEnzanBubunwa {
    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int v = sc.nextInt();
        int[] a = new int[n];

        for (int i = 0; i < n; i++) {
            a[i] = sc.nextInt();

        }
        /* N個の数字の中から、１つ以上選ぶ組合せを全探索したい。
        * 全探索のパターン数は下記。
        * 例：N=3 (1 << 3) = 2の3乗 = 8; ３個の数字の選択パターンは全部で８通り。
        * 
        * 問題に合わせて読み替えると
        * N個の整数が与えられたので、全探索するには何通り調べればよいか知りたい。
        * (1 << N)がパターン数 = ２のN乗
        * 
        * 次に（1 << N)パターンで全探索する方法を考える。
        * ３つの数字を選択するパターンは下記の通り。１が選択。０が選択しない。
        * 
        * {2, 1, 0}←選択される数字の集合
        *  0  0  0 
        *  0  0  1
        *  0  1  0
        *  0  1  1
        *  1  0  0
        *  1  0  1
        *  1  1  0
        *  1  1  1
        *  
        *  この８通り。これをビット演算で実現したい。
        *  これは下記のAND演算で実現する。
        *  index & (1 << 配列の添字番号) != 0
        *  上記の意味→　「indexの2進数」AND「 (1 << 配列の添字番号)の2進数」で0以外
        *  例えば index=7で N=1なら１０進数で「７」と「２」。
        *  ２進数「0111」AND「0010」= 「0010」=10進数の「２」
        *  
        *  例
        *  index=1 & (1 << 配列の添字番号＝0) != 0が成立するので、配列(0)を選択
        *  index=1 & (1 << 配列の添字番号＝1) != 0が成立しないので、配列（１）は選択しない
        *  index=1 & (1 << 配列の添字番号＝2) != 0が成立しないので、配列（２）は選択しない
        *  ・
        *  index=2 & (1 << 配列の添字番号＝0) != 0が成立しないので、配列（0）は選択しない
        *  index=2 & (1 << 配列の添字番号＝1) != 0が成立するので、配列（1）は選択
        *  index=2 & (1 << 配列の添字番号＝2) != 0が成立しないので、配列（2）は選択しない
        *  ・
        *  ・
        *  ・
        *  index=7 & (1 << 配列の添字番号＝0) != 0が成立するので、配列(0)を選択
        *  index=7 & (1 << 配列の添字番号＝1) != 0が成立するので、配列(1)を選択 
        *  index=7 & (1 << 配列の添字番号＝2) != 0が成立するので、配列(2)を選択 
        *  こんな感じで全探索する。
        *  
        *  簡単に言うと、８通り全探索したいなら
        *  0～8を順番に2進数に変換して、１になったとこだけ選択する。
        *  
        *  下記コードに読み替えると
        *  for文1重目の　S = index
        *  for文2重目の　i = 配列の添字番号
        *  
        */


        for (int S = 0; S < (1 << n); S++) {//探索数＝２のN乗
            int total = 0;
            
            for (int i = 0; i < n; i++) {
                if((S & (1 << i)) != 0) {// index & (1 << 配列の添字番号) != 0が成立するなら配列(n)を選択
                    total += a[i];
                }
            }

            if(total == v) {
                System.out.println("Yes");
                return;
            }
        }
        
        System.out.println("No");


    }
}

Python

簡単に言うと、８通り全探索したいなら、0～8を順番に2進数に変換して、１になったとこだけ選択する。

import itertools
N = 3
A=[1,2,3]

# 数列Aをビット全探索
def judge(bit):
    total = 0
    for i in range(N):
        if bit[i]:# if文の判定では、0はFalse扱い、他の整数はTrue扱い
            print(A[i], end=" ")
    print()

# タプルの「0 or 1」でビット列を表現
# N＝3なら3ビット
for bit in itertools.product((0,1), repeat=N):
    print(bit)
    judge(bit)

#-------------------------------------------------------------------------------------------
# bit演算子を使うバージョン
N = 3
A=[1,2,3]

# 数列Aをビット全探索
def judge2(bit):
    for i in range(N):
        if(bit & (1 << i)):#整数bitを2進法とみなしたときの、下からi桁目が1か判定
            print(A[i], end=" ")
    print()

for bit in range(1 << N):#1~2のN乗
    print(bin(bit))
    judge2(bit)

グラフ典型問題

グラフ問題の考察や解法でよく使いそうなものをメモ。

連結成分の個数を数える

全ての頂点から探索を開始して、未探索のものがあれば、連結成分の個数としてカウント

例えば、下図の場合は１から探索開始。連結成分＋１。
↓
１，２，３が探索済みになる。
↓
２から探索開始→探索済みなのでスルー
↓
３から探索開始→探索済みなのでスルー
↓
４から探索開始→未探索なので連結成分＋１。

連結成分

サンプルコード（無向グラフ）

import sys
sys.setrecursionlimit(10**6)

# n=頂点数　m=辺の数
n, m = map(int, input().split())
g = [[] for _ in range(n)]
seen = [False]*n

def dfs(num):
    seen[num] = True
    for next in g[num]:
        if seen[next]:
            continue
        dfs(next)

# g[頂点番号][ここから繋がる頂点番号]
for i in range(m):
    a, b = map(int, input().split())
    g[a-1].append(b-1)
    g[b-1].append(a-1)

#連結成分の個数を数える
renketu = 0
for i in range(n):
    if not seen[i]:# 探索済みはスルー
        renketu +=1
        dfs(i)

print(renketu)

例題

連結成分の個数がわかれば解ける問題
C - Don’t be cycle

参考サイト

qiita.com

閉路検出

そのうち書きたい。

参考サイト

drken1215.hatenablog.com

木構造

木構造もグラフなんやで。

連結成分1個＆閉路なしのグラフが木構造。

頂点の深さ計測

木構造の深さ

DFSは、頂点を見つける度に関数が呼び出されるので、再帰関数の深さ＝頂点の深さになる。

import sys
sys.setrecursionlimit(10**6)

n = int(input())
tree = [[] for _ in range(n)]
parent = list(map(int, input().split()))

for i in range(n-1):
    tree[parent[i]].append(i+1)

depth = [0]*n

#深さ計測
def rec(vertex, count):
    depth[vertex] = count

    for child in tree[vertex]:
        rec(child,count+1)# 再帰の深さ＝深さ

rec(0, 0)

for ans in depth:
    print(ans)

参考サイト

頂点の深さ | アルゴ式

木 (グラフ理論) を徹底解説 〜 実装法から探索法まで 〜 | アルゴ式

最短経路＆経路復元＆距離計測

こっちに書いた。

dodosu.hatenablog.jp